-
In this project, I tackled the task of predicting housing prices using the California Housing Dataset . Instead of relying on pre-built linear regression implementations from libraries like Scikit-Learn or PyTorch, I chose to build the model from scratch, applying the closed-form solution of linear regression (Normal Equation). This hands-on approach deepened my understanding of the mathematical foundations behind linear regression while allowing me to control every step of the training process.
The workflow began with data preprocessing, where I shuffled the dataset, performed an 80-20 train-test split, and applied feature scaling using min-max normalization. I added a bias term to the feature matrix before calculating the weight vector analytically, ensuring that the model was built entirely from first principles. By avoiding black-box implementations, I gained valuable insight into how feature transformations, scaling, and bias terms influence model performance. To assess the model's effectiveness, I evaluated it using standard metrics: Mean Absolute Error (MAE) ,Mean Squared Error (MSE) , and Root Mean Squared Error (RMSE). The results were promising, with an RMSE of approximately 0.74 on the training set and 0.75 on the test set, indicating that the model generalized well to unseen data.
I also visualized the model's predictions against actual values and plotted the distribution of residuals. Importantly, I generated Q-Q plots to verify one of the core assumptions of linear regression: that errors should follow a roughly normal distribution. While the residuals were reasonably well-behaved, some deviations from normality suggested potential areasfor improvement, such as exploring polynomial features or regularization techniques to better capture non-linear relationships.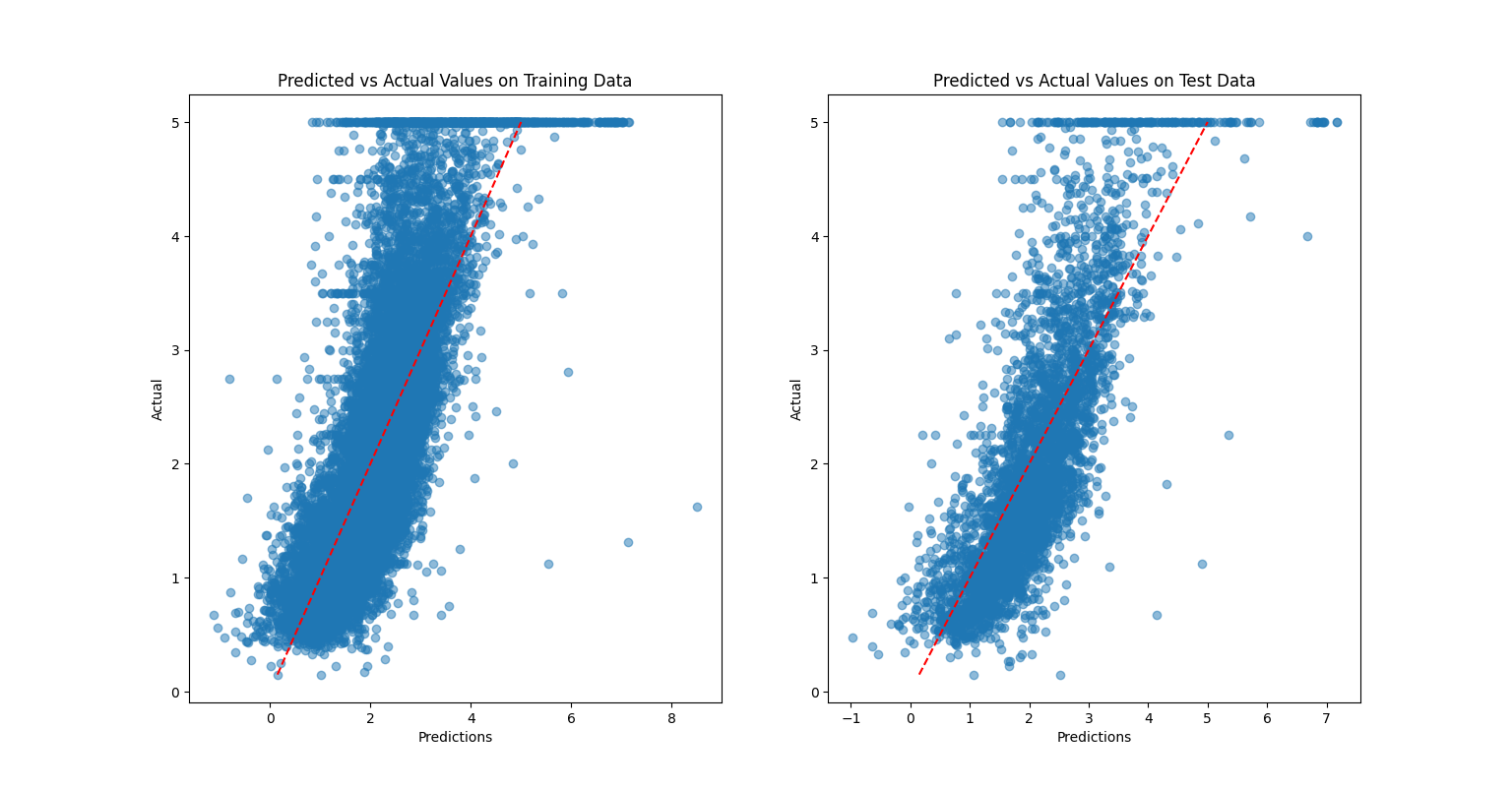
Figure 1: Predicted vs Actual values. 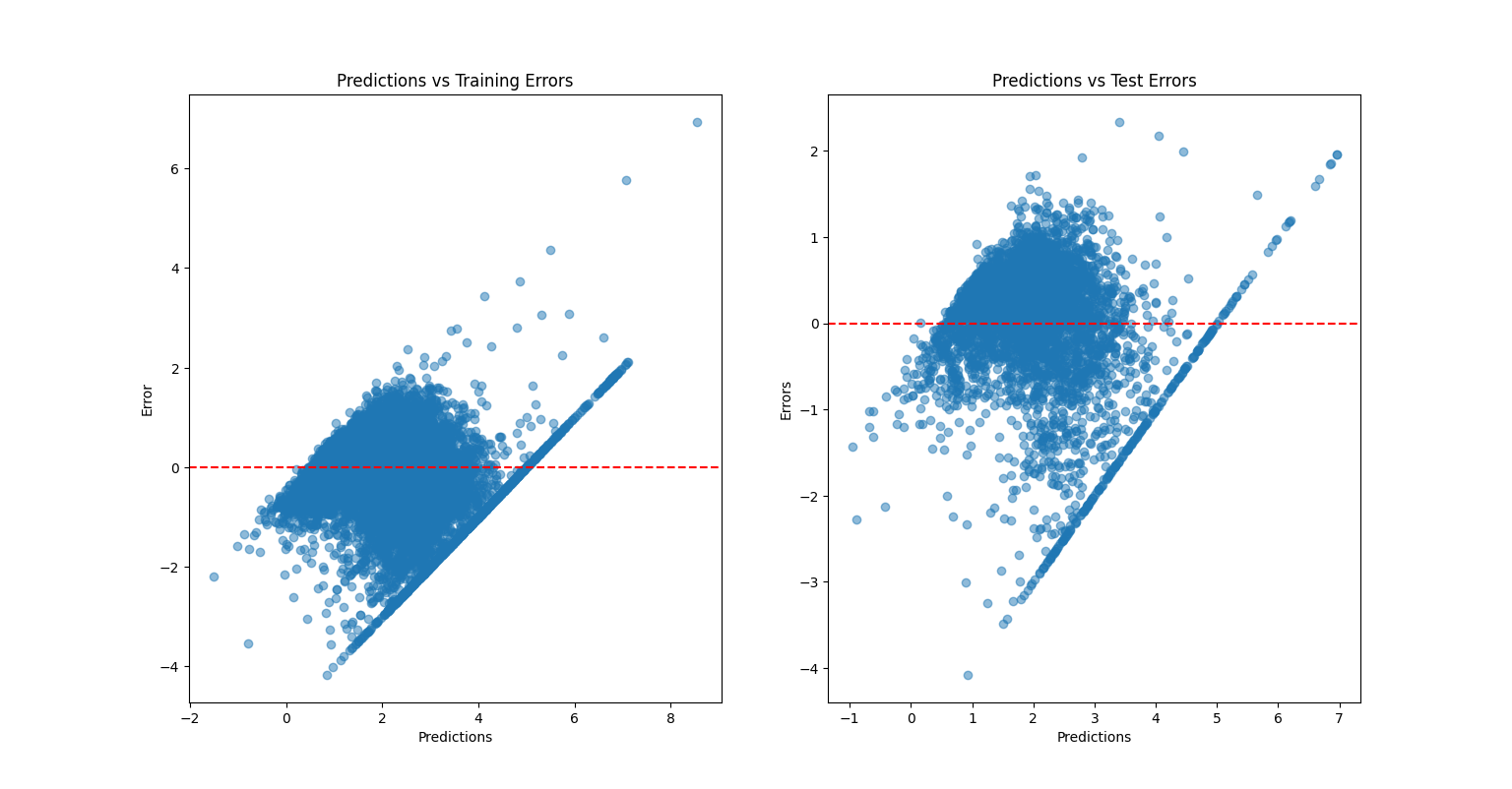
Figure 2: Predictions vs Errors. 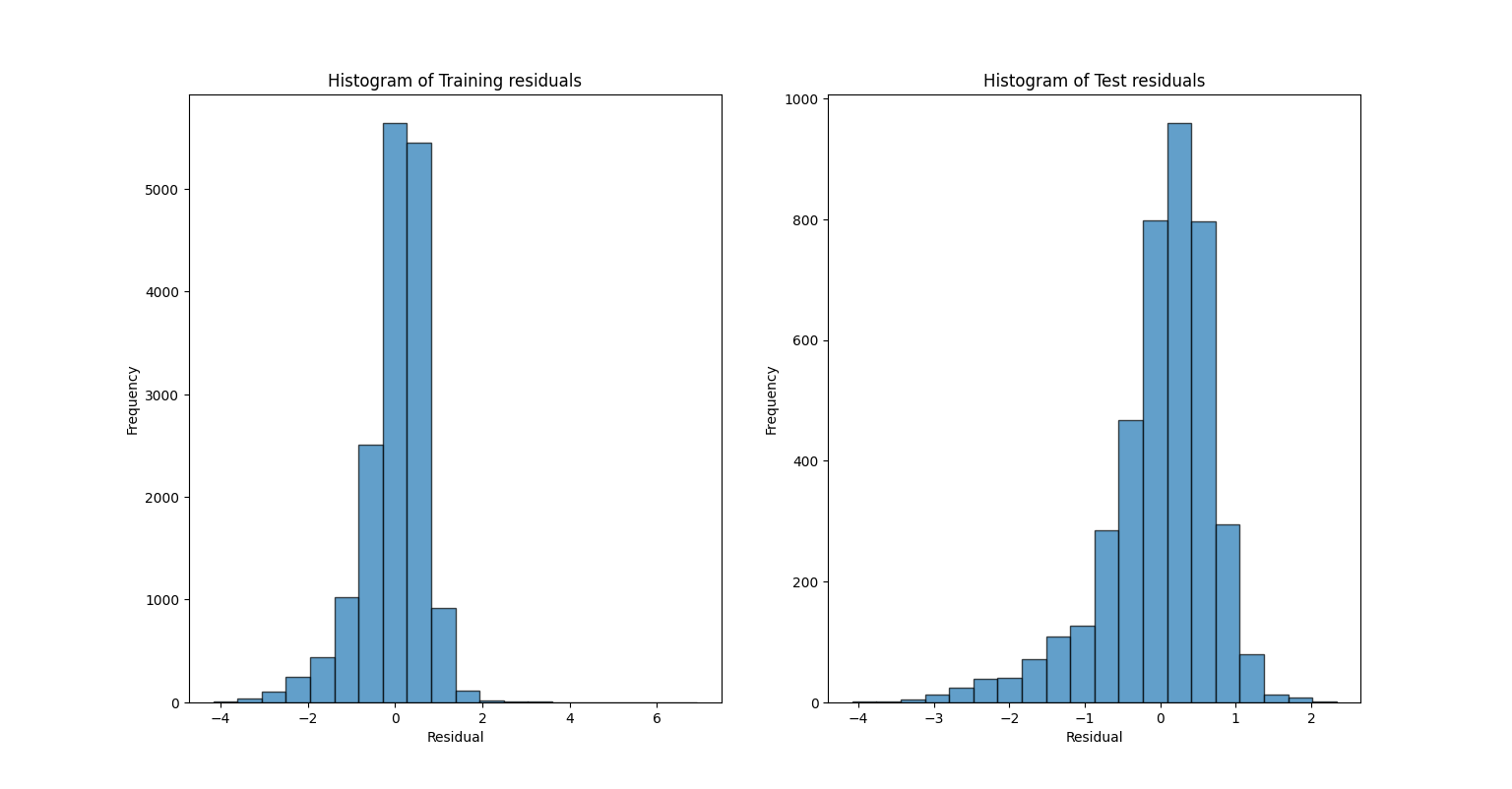
Figure 1: Error Distribution confirms approximate normality.. 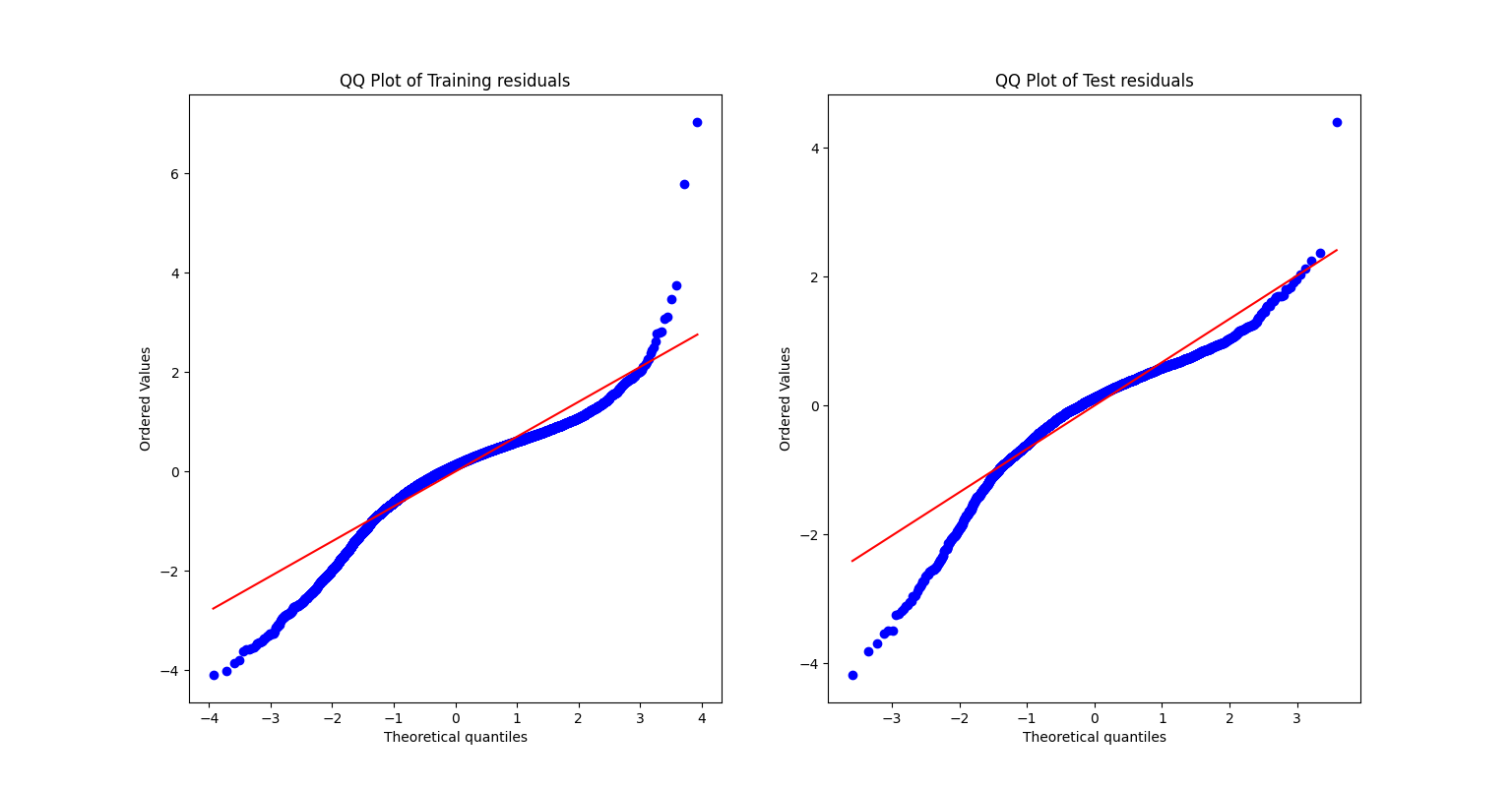
Figure 2: Q-Q Plot of Errors. Through this project, I not only built a functional predictive model but also gained a more intuitive grasp of linear regression's strengths and limitations. The process highlighted how theoretical understanding translates into practical application, while the residual analysis emphasized the importance of critically evaluating model assumptions rather than solely relying on performance metrics.
The code for this project can be found here.